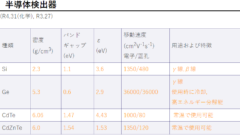
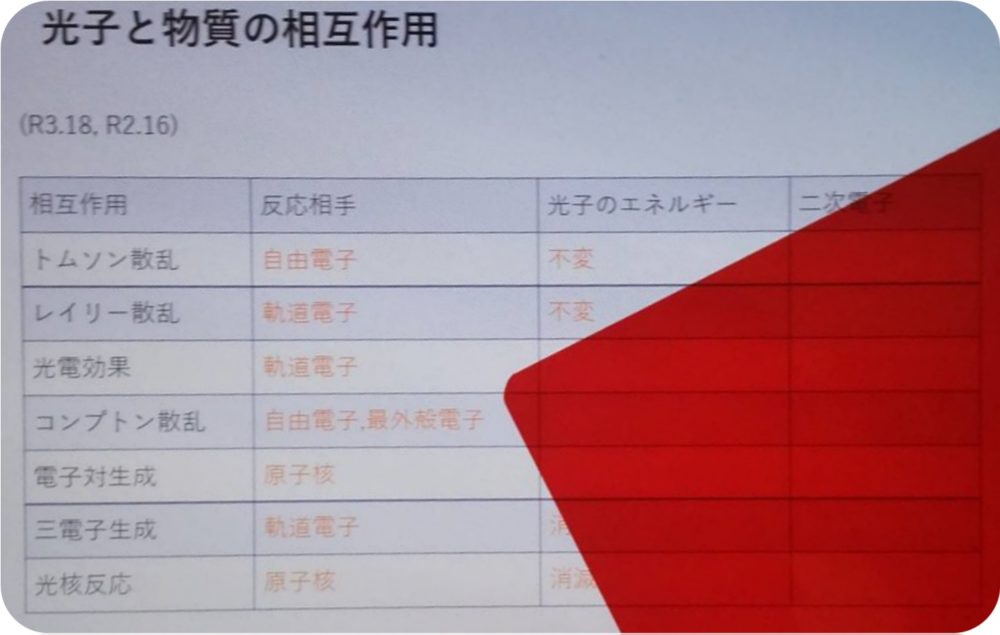
(R4.16, R3.18, R2.16)
| 相互作用 | 反応相手 | 光子のエネルギー | 二次電子 |
| トムソン散乱 | 自由電子 | 不変 | なし |
| レイリー散乱 | 軌道電子 | 不変 | なし |
| 光電効果 | 軌道電子 | 消滅 | 光電子 |
| コンプトン散乱 | 自由電子,最外殻電子 | 散乱 | 反跳電子 |
| 電子対生成 | 原子核 | 消滅 | 原子,陽電子 |
| 三電子生成 | 軌道電子 | 消滅 | 原子,陽電子 |
| 光核反応 | 原子核 | 消滅 | なし |
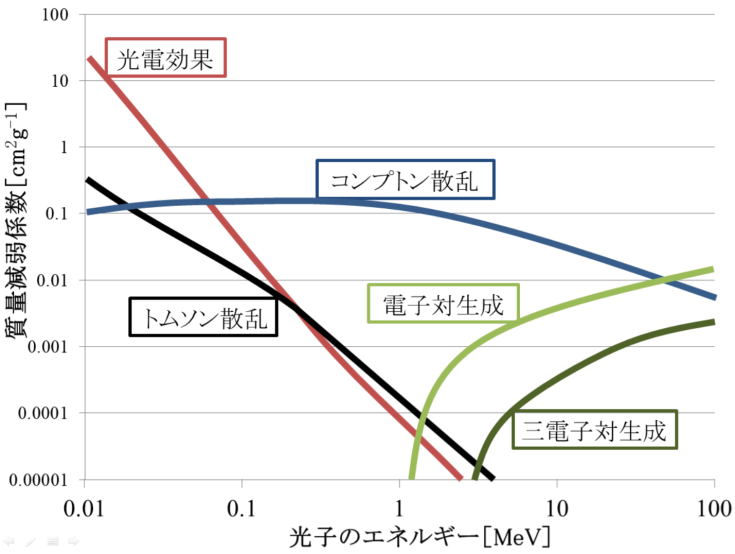
弾性散乱
・光子の波動性を示す反応
・トムソン散乱
自由電子との相互作用
光子のエネルギーは変化せず,進行方向が変化する
・レイリー散乱(干渉性散乱)
軌道電子との相互作用
光子のエネルギーは変化せず,進行方向が変化する
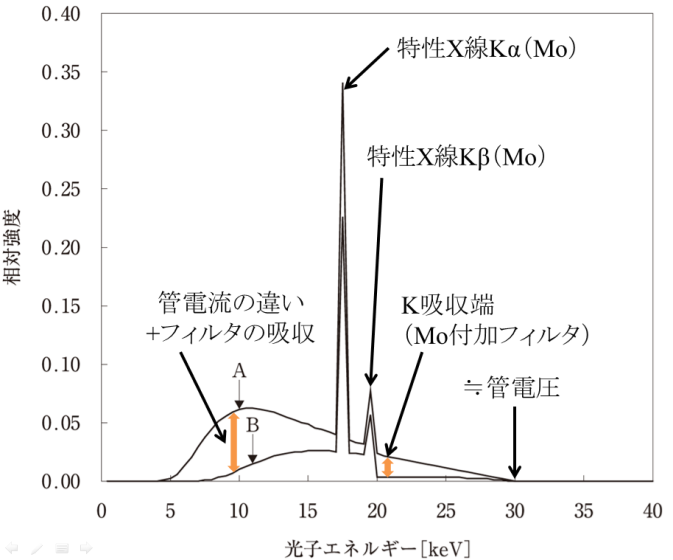
光電効果
(R5.16, R3.19.20)
・光子のエネルギーEe
Ee=Er‐Eb
Er:光子のエネルギー
Eb:軌道電子のエネルギー
・光電子エネルギー
K殻光電子<L殻光電子
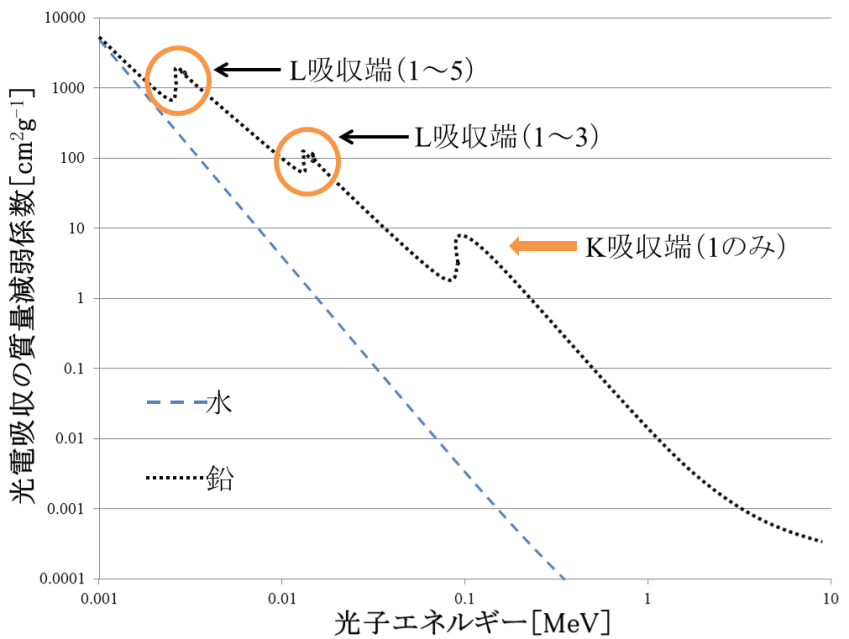
・吸収端 (R1.4)
光子のエネルギーが各殻の軌道電子放出に必要なエネルギーを上回り,減弱係数が急激に大きくなる場所
エネルギー:L吸収端 < K吸収端
K吸収端のエネルギー
:13.6×(Z-1)2[eV]
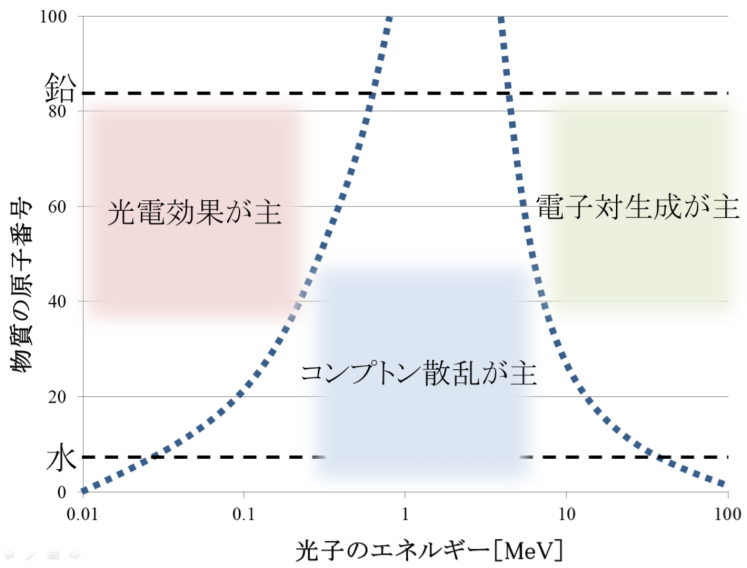
・反応断面積τ∝Z5×Er-3.5
Z:ターゲットの原子番号
・光子の粒子性を示す反応
・光電ピーク(全エネルギーピーク)
放出されたγ線がすべてのエネルギーを電子に与えて検出器に検出されるピーク
・入射光子のエネルギーがK殻電子電離エネルギーよりも大きい場合,光電子の80%がK殻光電子となる
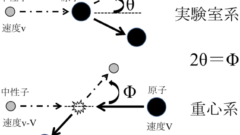
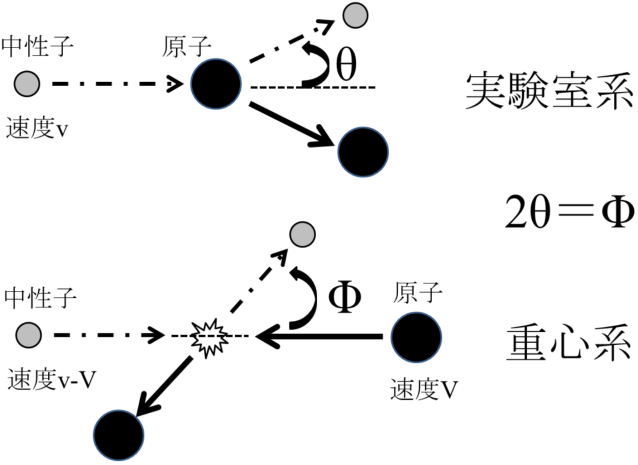
コンプトン散乱(非弾性散乱)
(R5.32, R4.18.19, R3.21.32, R1.17.18.20)
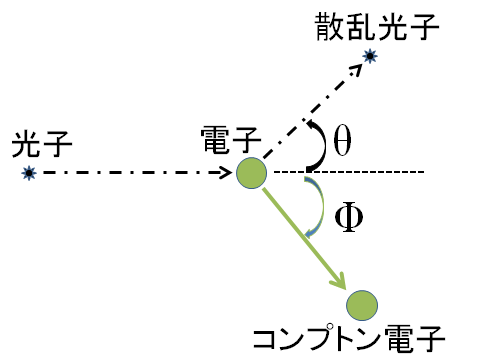
・散乱光子のエネルギーEr′
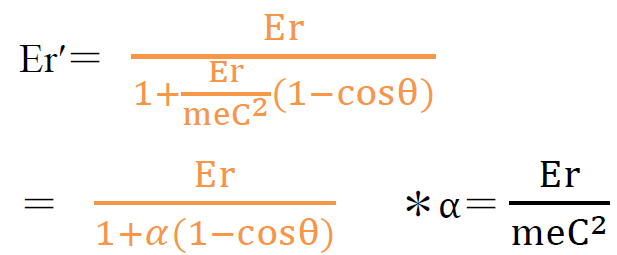
・コンプトン電子のエネルギーEe
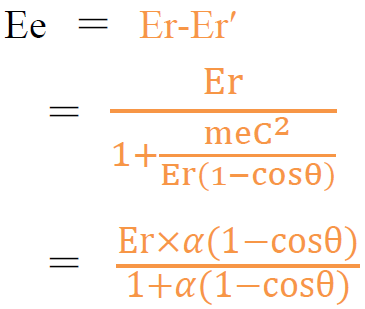
・Ee maxのとき,Er′min
(180度散乱:コンプトン端)
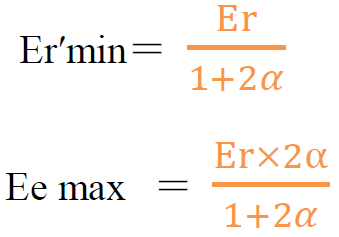
・Ee minのとき,Er′max
(0度散乱,反跳電子は90度散乱)
Er′max = Er
Ee min = 0
*θ:0~180度に散乱する
*Φ:0~90度に散乱する
*meC2:電子の静止エネルギー
・反応断面積σ∝Z
*面密度[g/cm2]が同じであれば物質によらない
・光子の粒子性を示す反応
・コンプトン連続部
コンプトン散乱で生じた反跳電子がとる0から最大エネルギーEmaxまでの連続分布
・コンプトン端
散乱角が180度の場合に電子に最もエネルギーを与えて,光子が検出器から出ていく場所
コンプトン連続部の終わり
・後方散乱ピーク
検出器以外で後方散乱した散乱光子(最小エネルギーとなっている)が検出されて生じるピーク
電子対生成
(R2.21,R1.19)
・光子(Er=hν)がクーロン場で消滅し,電子-陽電子対が生成される現象
入射光子のエネルギーEr
Er = 2meC2 + Krec +Kp + Ke
Krec:反跳粒子の運動エネルギー
(原子核の場合は≒0)
Kp + Ke:電子対の運動エネルギー
→電子対の運動エネルギーKp + Ke
Kp + Ke=Er – (2meC2+ Krec)
:KpとKeには連続的に分配される
・閾値:1.022[MeV]
・反応断面積κ∝Z2
三電子対生成
・電子のクーロン場で電子対生成が起こる現象
→電子×2+陽電子にエネルギーが連続的に分配される
・閾値:2.044[MeV]
(Krec=hν/2となるため)
光核反応
高エネルギーγ線が原子核に当たると,ある確率で吸収され,原子核を励起し,そのエネルギーが原子核内の 核子の結合エネルギーを超えると,核子は核外へ飛び出す
・光子の粒子性を示す反応
・反応断面積
:γ線のエネルギーが15~20MeVで最大
・(γ,p),(γ,n),(γ,d),(γ,α),(γ,fission)などの反応が起こる
(γ,n)は10~20MeVで起こりやすい
・閾値は存在し(だいたい結合エネルギーである8~10MeV程度),Q値は負
(回析)
・ブラッグの反射条件を満たした場合に,Xは回析する
→結晶の構造解析に利用
・光子の波動性を示す反応
光子エネルギーの伝達
(R5.18, R4.17, R3.32, R2.18)
・質量減弱係数μ/ρ
μ/ρ = (τ+σ+κ)×N÷ρ
N:1cm3中の原子数
ρ:物質の密度
・質量エネルギー転移係数μtr/ρ
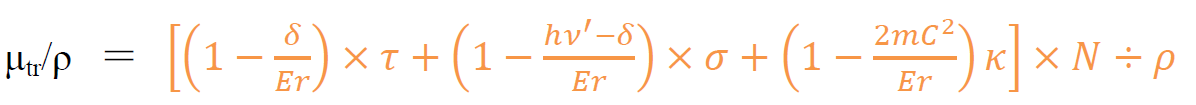
δ:特性X線の平均エネルギー
*各項はそれぞれ「光電効果」「コンプトン散乱」「電子対生成」で損失するエネルギーを表す
・質量エネルギー吸収係数μen/ρ
μen/ρ= μtr/ρ×(1‐G)
G:制動放射により失われる二次電子のエネルギーの割合
光子の減弱
(R5.15, R2.20,R1.30(化学))
・光子の強度I
I = I0×e-μx×B
I0:初期X線光子量
μ:線減弱係数(cm-1)
x:物質の厚さ(cm)
B:ビルドアップ係数
B=(全光子数)÷(直接光子数)
=1+(散乱光子数)÷(直接光子数)
半価層
(R3.32, R2.22)
・半価層X1/2
X1/2 = ln2/μ
= 0.693/μ
・1/10価層X1/10
X1/10 = ln10/μ
= 2.3/μ
・(第一)半価層H1
:線量が初めの半分となる吸収板の厚さ
・第二半価層H2
:さらに線量を半分とする厚さ
・均等度 = H1/H2
・不均等度 = H2/H1
*特性X線ではH1=H2となり,連続X線では均等度<1,不均等度>1




コメント