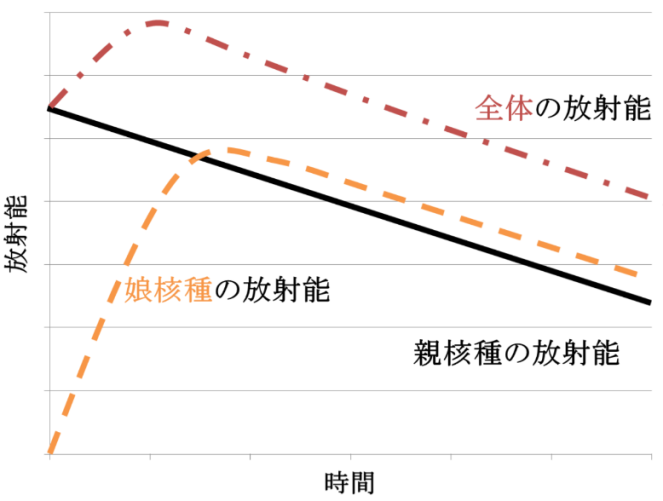
放射性壊変と放射能 / 核分裂

放射性壊変と放射能

(R5.5, R4.1.4.13, R3.14(生物), R3.19, R1.2.3.4)
・放射能A　
　A　＝　-dN/dt　＝　λ×N

・壊変定数λ
　λ　＝　log_e2/T　＝　0.693/T
　T：半減期
　
・原子数N　
(R5.1.3, R4.2(実務), R3.4)
　N　＝　w/W×6.02×10²³
　w：放射性物質の質量
　W：対象物質の原子量
　w/W：モル数
　6.02×10²³：アボガドロ定数

・分岐比　 (R2.1,R1.2.7(物理))
　λ＝λ1+λ2+λ3+……　
　λ1，λ2，λ3：部分半減期
　分岐比　→　λ1：λ2＝T2：T1

・平均寿命τ
　τ＝1/λ＝1.44×T

・壊変図
(R4.17)

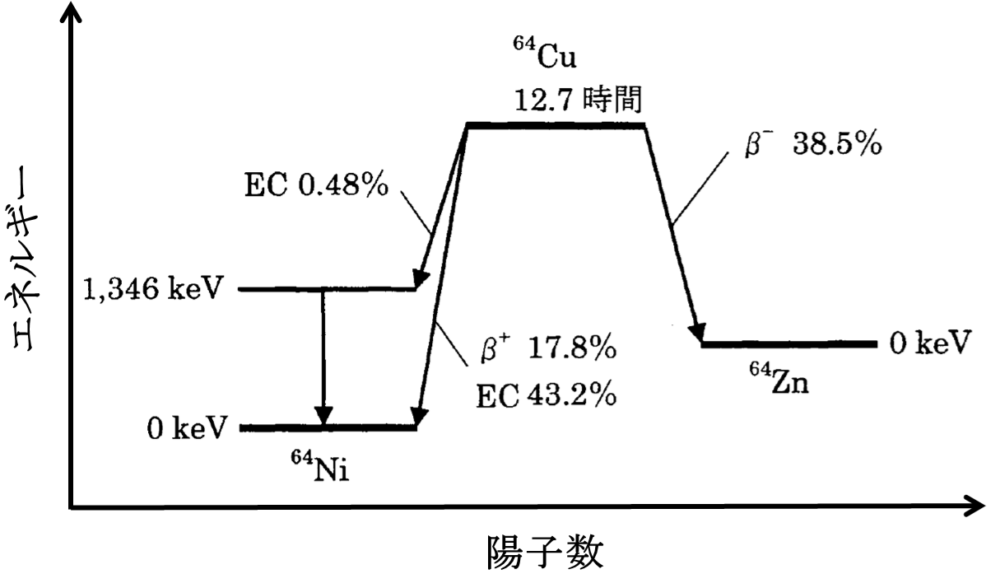
放射性壊変の方法に関してはこちら↓
「対策ノート：放射性壊変」

放射性壊変

(R5.3, R3.6, R2.7) α壊変 (R4.20, R2.8.12,R1.6.31) 　(A，Z)　→　(A-4，Z-2)　+　α ・親核種からα粒子が飛び出す ・壊変条件 ：Q＞0 　Q値＝｛M親－(m娘+α)｝×C2 　M親：親核種の質量　 　m娘：娘核種の質量　 　C：光速 ・エネルギー保存則　 (R3.31) 　Q＝1/2×mαvα2　+　1/2×m娘v娘2 ・運動量保存則　 (R4.12, R3.31) 　m娘v娘＝mαvα ・α粒子のエネルギーEα 　Eα＝1/2×mαvα2 　Eα＝m娘 / (m娘+mα)×Q →α線は線スペクトルのエネルギーをもつ →Eαはトンネル効果(量子力学的説明)によってクーロン障壁を超える ・生成核の反跳エネルギーEb (R3.13) 　Eb＝mα/ (m娘+mα)×Q 　　　＝(mα/ m娘)×Eα ・ガイガー・ヌッタルの法則　 　放出されるα粒子のエネルギーと崩壊定数の経験的関係を示す式 　短い半減期の核種からのα線エネルギー>長い半減期の核種からのα線エネルギー β－壊変 　(R2.32) 　(A，Z)　→　(A，Z+1)　+　...

supervisor.radiological.site

放射線計測で得られる計数

　(R1.5(物理))
・t0からt秒までの壊変数T
　T＝N×(1-e^-λt)　＝　A0/λ×(1-e^-λt)
　A0,N0：t0の時の放射能,原子数

・t秒計測したときの検出される確率p
　p＝ε×(1-e^-λt)
　ε：検出効率

自発核分裂

　(R1.11)
　α壊変と同様に,トンネル効果によっておこる
代表核種：「²³⁵U」「²³⁸U」「²³⁹Pu」「²⁴⁰Pu」

誘導核分裂

　親燃料物質+速中性子
→核分裂性物質+速中性子or熱中性子

　核分裂
→核分裂生成物+核分裂片

・即発中性子
：核分裂直後に放出される中性子

・遅発中性子
：核分裂後にやや遅れて放出される中性子

核分裂生成物

(R5.11, R4.8, R2.9)
・²³⁵U分裂　²³⁵U(n)
：「¹³⁷Cs」「⁹⁰Sr」「⁹⁹Mo」「¹³¹I」「¹³³Xe」
　平均2.5個2MeV程度の中性子が放出される
　核分裂の収率の極大は原子量95または138付近
　原子番号138付近の生成物は中性子過剰核となる